 11
11 F1
F1 C2
C2 L7
L7 L8
L8 05
05 74
74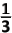 n3
n3
 E5
E5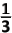 n3
n3
 50
50 51
51 52
52 N2
N2 53
53 54
54 55
55 56
56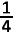 n² (n − 4)
n² (n − 4)
 57
57 K0
K0 58
58 66
66 71
71 75
75 85
85 92
92
 93
93
 Q5
Q5
 94
94
 H1
H1 98
98 A4
A4 C6
C6 B6
B6 B8
B8 C3
C3 D0
D0
 D7
D7
 D9
D9
 E3
E3 E9
E9 F6
F6 F9
F9 G1
G1 G8
G8 I1
I1 I9
I9Klik op de formule en het bewijs komt rechts
| n ! > 2n |  11 11 |
| 2n > n3 ( n = 10,11,...) |  F1 F1 |
| n² − n > 9n − 1 ∀ n > 9 |  C2 C2 |
| ∀ n > 5 : (n + 1)2 < 2n |  L7 L7 |
|
∀ n > 10 : n − 2 < |  L8 L8 |
|
|  05 05 |
|
|  74 74 |
12 + 22 + 32 + ... + (n − 1)2
< 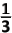 n3 n3
|  E5 E5 |
12 + 22 + 32 + ... + n2
> 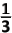 n3 n3
|  50 50 |
|
|  51 51 |
| n3 > (n + 5)2 vanaf n = ? |  52 52 |
| 4n−1 > n2 vanaf n = 3 |  N2 N2 |
| de ongelijkheid van Bernoulli |  53 53 |
|
|  54 54 |
| 1,1n > 2n voor n = 21, 22, ... |  55 55 |
|
|  56 56 |
0² + 1² + 2² + ... + (n − 1)² > 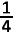 n² (n − 4) n² (n − 4)
|  57 57 |
|
|  K0 K0 |
|
|  58 58 |
| (2n) ! > 2n. (n !)2 voor n = 2, 3, ... |  66 66 |
| n ! < nn voor n = 2, 3, 4, ... |  71 71 |
|
|  75 75 |
|
|  85 85 |
|
|  92 92 |
|
|   93 93 |
|
|   Q5 Q5 |
|
|   94 94 |
|
|   H1 H1 |
|
|  98 98 |
|
|  A4 A4 |
| (2n) ! < 4n.(n !)2 (n=1,2,3,...) |  C6 C6 |
|
|  B6 B6 |
| 2!.4!.6!...(2n)! > [ (n+1)! ]n (n=2,3,...) |  B8 B8 |
|
|  C3 C3 |
|
|  D0 D0 |
|
|   D7 D7 |
| 2n−1. n! ≤ nn (n=1,2,3,...) |   D9 D9 |
|
|   E3 E3 |
|
|  E9 E9 |
|
|  F6 F6 |
| 5n ≥ 3n + 4n (n = 2,3,...) |  F9 F9 |
| 5n+1 + 3n+1 > 22n+1 |  G1 G1 |
|
|  G8 G8 |
|
|  I1 I1 |
|
|  I9 I9 |
V o l l e d i g e
i n d u c t i e
Mathematical induction (Engels)
Vollständige Induktion (Duits)
Induction Mathématique (Frans)
Indução matemática (Portugees)
Induzione matematica (Italiaans)
Inducción completa (Spaans)
→ telling vanaf 1 jan. 2021 ←